[백준] 동전 바꿔주기 (2624번)

문제

명보네 동네 가게의 현금 출납기에는 k 가지 동전이 각각 n1, n2, … , nk개 씩 들어있다. 가게 주인은 명보에게 T원의 지폐를 동전으로 바꿔 주려고 한다. 이때, 동전 교환 방법은 여러 가지가 있을 수 있다. 예를 들어, 10원 짜리, 5원 짜리, 1원 짜리 동전이 각각 2개, 3개, 5개씩 있을 때, 20원 짜리 지폐를 다음과 같은 4가지 방법으로 교환할 수 있다.

• 20 = 10×2 
• 20 = 10×1 + 5×2 
• 20 = 10×1 + 5×1 + 1×5 
• 20 = 5×3 + 1×5

입력으로 지폐의 금액 T, 동전의 가지 수 k, 각 동전 하나의 금액 pi와 개수 ni가 주어질 때 (i=1, 2,…, k) 지폐를 동전으로 교환하는 방법의 가지 수를 계산하는 프로그램을 작성하시오. 방법 의 수는 231-1을 초과 하지 않는 것으로 가정한다.

입력

첫째 줄에는 지폐의 금액 T(0＜T ≤ 10,000), 둘째 줄에는 동전의 가지 수 k(0＜k ≤ 100), 셋째 줄부터 마지막 줄까지는 각 줄에 동전의 금액 pi(0＜pi ≤ T)와 개수 ni(0＜ni ≤ 1,000)가 주어진다. pi와 ni사이에는 빈칸이 하나씩 있다.

출력

첫째 줄에 동전 교환 방법의 가지 수를 출력한다. 방법이 없을 때는 0을 출력한다.

예제 입력 1 복사

20 3 5 3 10 2 1 5

예제 출력 1 복사

4

---

까다로운 dp 문제였다.

dp를 2차원으로 선언해 dp[i][j] : i번째 동전까지 사용해서 j원을 만드는 경우의 수로 둔다.

그리고 각 동전 순서별로 가능한 경우의 수를 구한다.

 

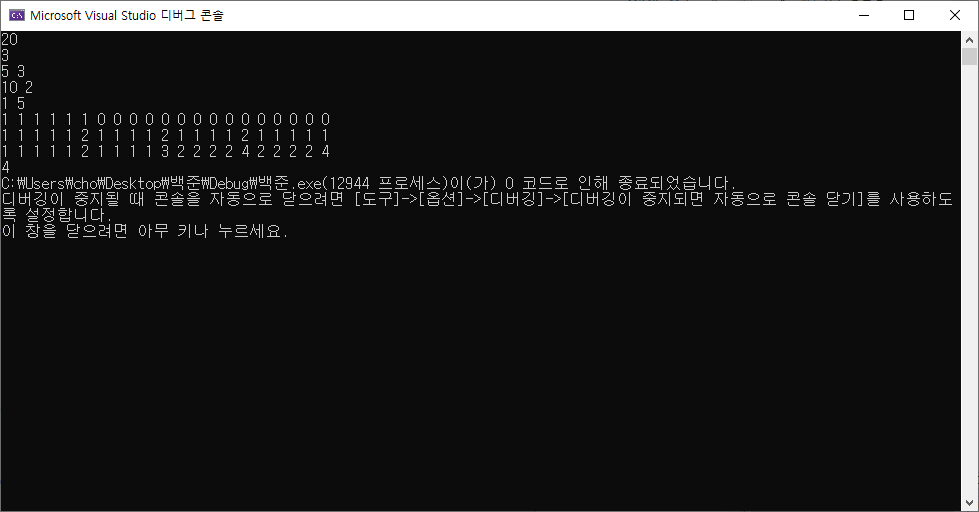
위는 예제 코드에서의 dp[i][j]를 구한 것이다. i는 1부터 3까지, j는 0원부터 20원까지이다.

정답 4가 뜨는 것을 볼 수 있다.

 

코드 원본 : https://github.com/chosh95/STUDY/blob/master/BaekJoon/2020/%EB%8F%99%EC%A0%84%20%EB%B0%94%EA%BF%94%EC%A3%BC%EA%B8%B0.cpp

chosh95/STUDY

C++ 코드

#include <iostream>
#include <algorithm>
using namespace std;
int T, K;
pair<int,int> p[101]; // p[i] = <금액, 개수>
int dp[101][10001]; // i번째 동전까지 사용해서 cost를 만드는 경우의 수

int main()
{
	cin >> T;
	cin >> K;
	for (int a, b, i = 1; i <= K; i++) {
		cin >> a >> b;
		p[i] = { a,b };
	}
	sort(p+1, p + K+1);
	dp[0][0] = 1;
	for (int i = 1; i <= K; i++) {
		for (int j= 0; j <= p[i].second; j++) {
			for (int k = 0; k <= T; k++) {
				if (p[i].first * j + k > T) break;
				dp[i][k + p[i].first *j] += dp[i-1][k];
			}
		}
	}

	cout << dp[K][T];
}