문제
서기 2116년, 인간은 더 이상 AI의 상대가 되지 못하게 되었다. 근력, 순발력, 창의력, 사고력, 문제해결능력, 심지어 인간미조차 AI가 인간을 앞선다. AI가 온 지구를 관리하며 이미 인류는 지구의 주인 자리에서 쫓겨난지 오래이다. 그나마 다행인 것은 AI가 인간을 적대적으로 대하지 않고, 도리어 AI가 쌓아올린 눈부신 기술의 발전으로 모든 사람이 무제한적인 재화를 사용할 수 있게 되어 한 세기 전의 사람들이 바라던 돈 많은 백수와 같은 삶을 누릴 수 있게 됐다는 사실이다. 대다수의 인간들은 현재의 상황에 만족하고 더 이상 발전을 포기한 채 놀고 먹으면서 시간을 보내고 있지만 일부 인간들은 인류의 영광을 되찾기 위해 저항군을 조직해 AI에게 투쟁하고 있다.
저항군은 AI에게 승산이 있는 종목을 찾고 있다. 이러한 종목을 가지고 AI에게 승부를 걸어 전 인류에게 도전정신과 인간의 위대함을 증명하고 싶기 때문이다. 저항군의 지도부는 무려 12시간에 걸쳐 AI에게 승산이 있는 종목을 찾기 위한 회의를 진행했다. 회의에서 알고리즘 문제 풀이 대결, 가위불바위총번개악마용물공기보스펀지늑대나무사람뱀 게임, 캐치마인드, 알까기, 스타크래프트, 똥 피하기 게임, 딸기 2비트, 딸기수박당근참외메론 게임, 백일장, 사생 대회 등 다양한 아이디어가 나왔지만 단 0.01%라도 승산이 있어 보이는 종목은 하나도 없었다.
그렇게 모두가 낙담하던 중 누군가가 역사책을 뒤져 인간이 AI에게 승산이 있는 종목을 찾아냈다. 바로 정확히 100년 전에 있었던 이세돌과 알파고의 바둑 대결이었다. 물론 알파고는 그 이후로 발전을 거듭했기에 바둑에서의 승산은 없지만 바둑의 룰을 변형한 Baduk2라는 종목에서는 이세돌이 알파고에게 한 세트를 이긴 것과 같이 인간이 AI에게 승산이 있다고 판단했다.
Baduk2의 룰은 바둑과 거의 유사하지만 양 선수가 돌을 1개씩 번갈아 두는 것이 아니라 2개씩 둔다는 점이 다르다. 서술의 편의를 위해 상하좌우로 인접한 같은 색 돌의 집합을 그룹이라고 하자. 아래의 판에서는 흑의 그룹과 백의 그룹이 각각 3개씩 존재한다.

Baduk2에서는 일반적인 바둑과 동일하게 자신의 돌로 상대방의 그룹을 빈틈없이 에워싸면 갇힌 돌을 죽일 수 있다. 어느 그룹이 빈틈없이 에워싸였다는 것은 그 그룹 내에 빈 칸과 인접해있는 돌이 하나도 없다는 것과 동치이다.
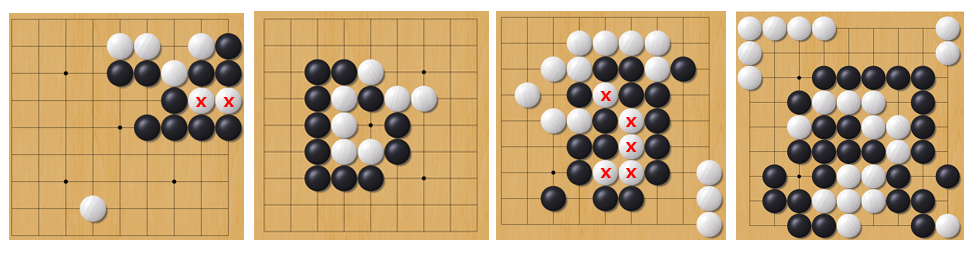
그리고 Baduk2에서는 모든 비어있는 칸에 돌을 둘 수 있다. 설령 상대 돌로 둘러싸여 있어 스스로 잡히는 곳이라고 하더라도 상관이 없다. 아래와 같은 상황을 생각해보자.

두 빨간 칸 모두 백의 입장에서 착수할 경우 연결된 그룹이 흑돌로 둘러싸이게 되어 원래 바둑의 규칙에서는 백의 입장에서 스스로 잡히는 곳이지만 Baduk2에서는 이와 무관하게 백이 빨간 칸 두 곳에 착수해 8개의 흑돌이 들어있는 그룹의 돌을 죽일 수 있다.
저항군은 AI에게 Baduk2로 도전장을 내밀었고 AI는 의외로 순순히 도전을 받아들였다. 이제 저항군은 2116년 3월 9일, 인류의 자존심을 건 Baduk2 대결을 시작한다. 그리고 당신에게 인류의 승리를 돕기 위해 현재 판 위에서 돌 2개를 두어 상대 돌을 최대한 많이 죽이게끔 하는 프로그램을 작성하는 임무가 주어졌다. 인류의 명예를 걸고 현재 판이 주어질 때 돌 2개를 두어 죽일 수 있는 상대 돌의 최대 갯수를 구하는 프로그램을 작성하자.
입력
첫째 줄에 바둑판의 행의 갯수와 열의 갯수를 나타내는 N(3 ≤ N ≤ 20)과 M(3 ≤ M ≤ 20)이 한 칸의 빈칸을 사이에 두고 주어진다. 그 다음 N개의 줄에는 각 줄마다 배열의 각 행을 나타내는 M개의 정수가 한 개의 빈 칸을 사이에 두고 주어진다. 각 칸에 들어가는 값은 0, 1, 2이다. 0은 빈 칸, 1은 나의 돌, 2는 상대의 돌을 의미한다. 빈 칸이 2개 이상 존재함과 현재 바둑판에서 양 플레이어 모두 상대방의 돌로 빈틈없이 에워싸인 그룹이 없음이 모두 보장된다.
출력
첫째 줄에 현재 판에서 돌 2개를 두어 죽일 수 있는 상대 돌의 최대 갯수를 출력한다.
예제 입력 1 복사
3 4 2 0 0 0 0 0 0 0 0 0 0 2
예제 출력 1 복사
1
바둑을 활용한 알고리즘 문제이다.
주어진 바둑판에서 흰 돌을 2개 놓아서 최대한 많이 잡을 수 있는 흑돌의 수를 구해야 한다.
바둑판의 크기가 최대 20x20이기 때문에 완전 탐색이 가능하다.
따라서 바둑판에서 0인 곳의 모든 위치 좌표를 벡터에 넣어서, 해당 벡터에서 2개씩 고른다.
선택한 2개의 위치에 흰 돌을 둔 후 그 상황에서 최대 몇 개의 흑돌을 잡을 수 있는지 계산하면 된다.
잡을 수 있는 흑돌의 갯수는 bfs를 이용했다. 방문하지 않은 흑돌의 위치를 매개변수로 받아서 연결된 모든 흑돌을 방문한다. 방문할 때 흑돌에 인접한 곳에 빈 곳이 있으면 해당 흑돌을 잡을 수 없기 때문에 0을 반환한다.
주의할 점은 연결된 모든 흑돌을 방문한 후에 0을 반환해야 한다는 것이다. 그렇지 않을 경우 틀린 답을 구하게 된다.
코드 원본 : https://github.com/chosh95/STUDY/blob/master/BaekJoon/2020/Baaaaaaaaaduk2%20(16988%EB%B2%88).cpp
chosh95/STUDY
프로그래밍 문제 및 알고리즘 정리. Contribute to chosh95/STUDY development by creating an account on GitHub.
github.com
C++ 코드
#include <iostream>
#include <memory.h>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
int N, M;
int p[21][21];
int visit[21][21];
int dx[4] = { -1,0,0,1 };
int dy[4] = { 0,-1,1,0 };
vector<pair<int, int>> zeroPos;
int bfs(int a, int b) {
queue<pair<int, int>> q;
q.push({ a,b });
visit[a][b] = 1;
int cnt = 0;
bool isPossible = true;
while (!q.empty()) {
int x = q.front().first;
int y = q.front().second;
q.pop();
cnt++;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx < 1 || ny < 1 || nx > N || ny > M) continue;
if (visit[nx][ny] == 1) continue;
if (p[nx][ny] == 0) isPossible = false;
else if (p[nx][ny] == 1) continue;
else if (p[nx][ny] == 2) {
q.push({ nx,ny });
visit[nx][ny] = 1;
}
}
}
if (!isPossible) return 0;
return cnt;
}
int main()
{
cin >> N >> M;
for (int i = 1; i <= N; i++)
for (int j = 1; j <= M; j++) {
cin >> p[i][j];
if (p[i][j] == 0) zeroPos.push_back({ i,j });
}
int res = 0;
for (int i = 0; i < zeroPos.size(); i++) {
for (int j = i + 1; j < zeroPos.size(); j++) {
p[zeroPos[i].first][zeroPos[i].second] = 1;
p[zeroPos[j].first][zeroPos[j].second] = 1;
int cnt = 0;
memset(visit, 0, sizeof(visit));
for (int a = 1; a <= N; a++) {
for (int b = 1; b <= M; b++) {
if (p[a][b] == 2 && visit[a][b] == 0) {
cnt += bfs(a, b);
}
}
}
res = max(res, cnt);
p[zeroPos[i].first][zeroPos[i].second] = 0;
p[zeroPos[j].first][zeroPos[j].second] = 0;
}
}
cout << res;
}'알고리즘 > 백준' 카테고리의 다른 글
| [백준] 팰린드롬 만들기 (1254번) (0) | 2020.10.07 |
|---|---|
| [백준] 오등큰수 (17299번) (0) | 2020.09.21 |
| [백준] 벽 부수고 이동하기 4 (16946번) (0) | 2020.09.16 |
| [백준] 사탕 게임 (3085번) (0) | 2020.09.02 |
| [백준] 숫자의 신 (1422번) (0) | 2020.09.02 |