세그먼트 트리는 여러개의 나열된 자료가 있을 때 그 자료를 구간에 따라 빠르게 값을 구할 때 사용되는 트리이다.
예를 들어 크기가 10인 배열이 있을 때 2~6번째 자료들의 합을 구하려면 보통 일일이 더해야 하지만 이 트리를 이용하면 빠르게 값을 가져올 수 있다.
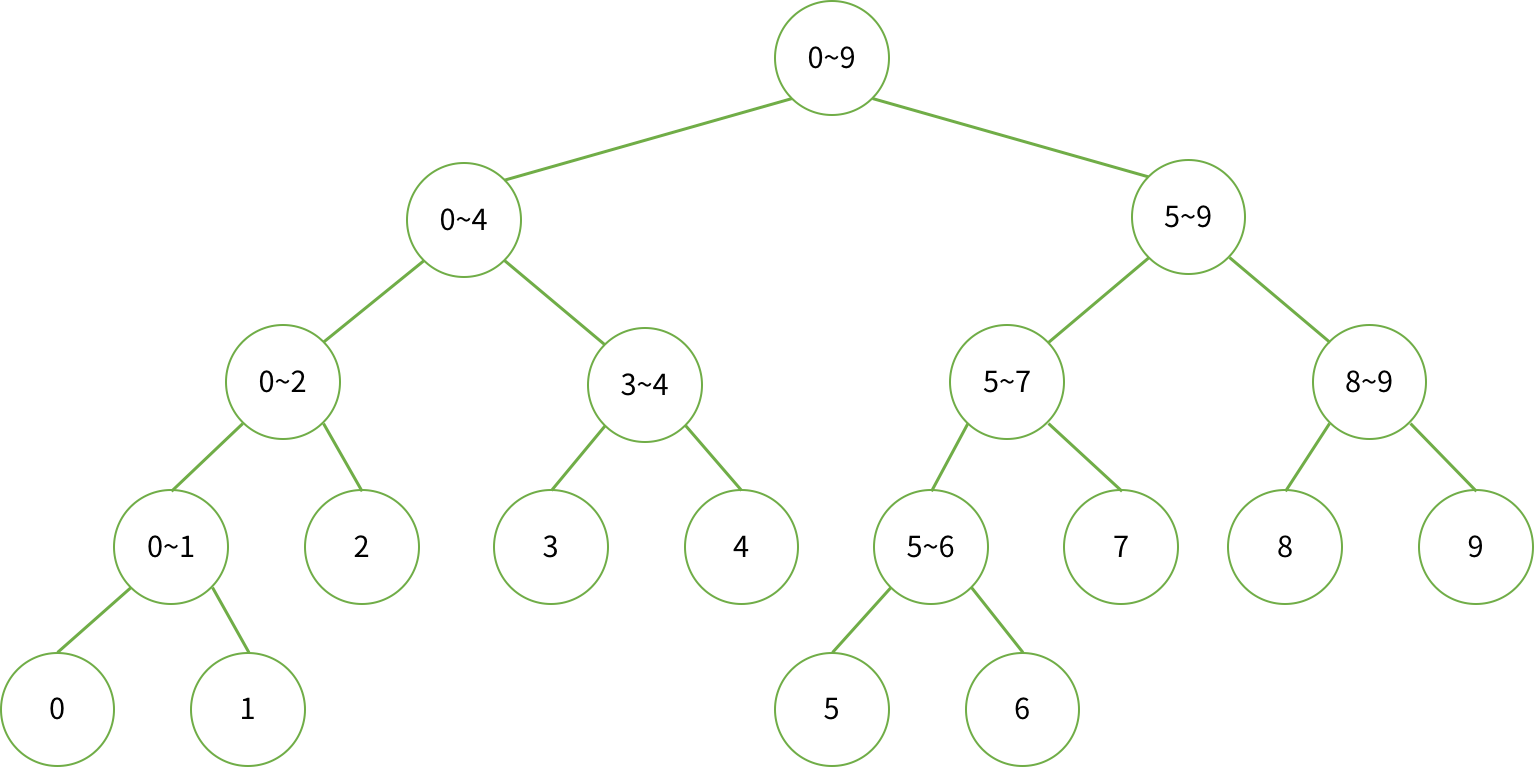
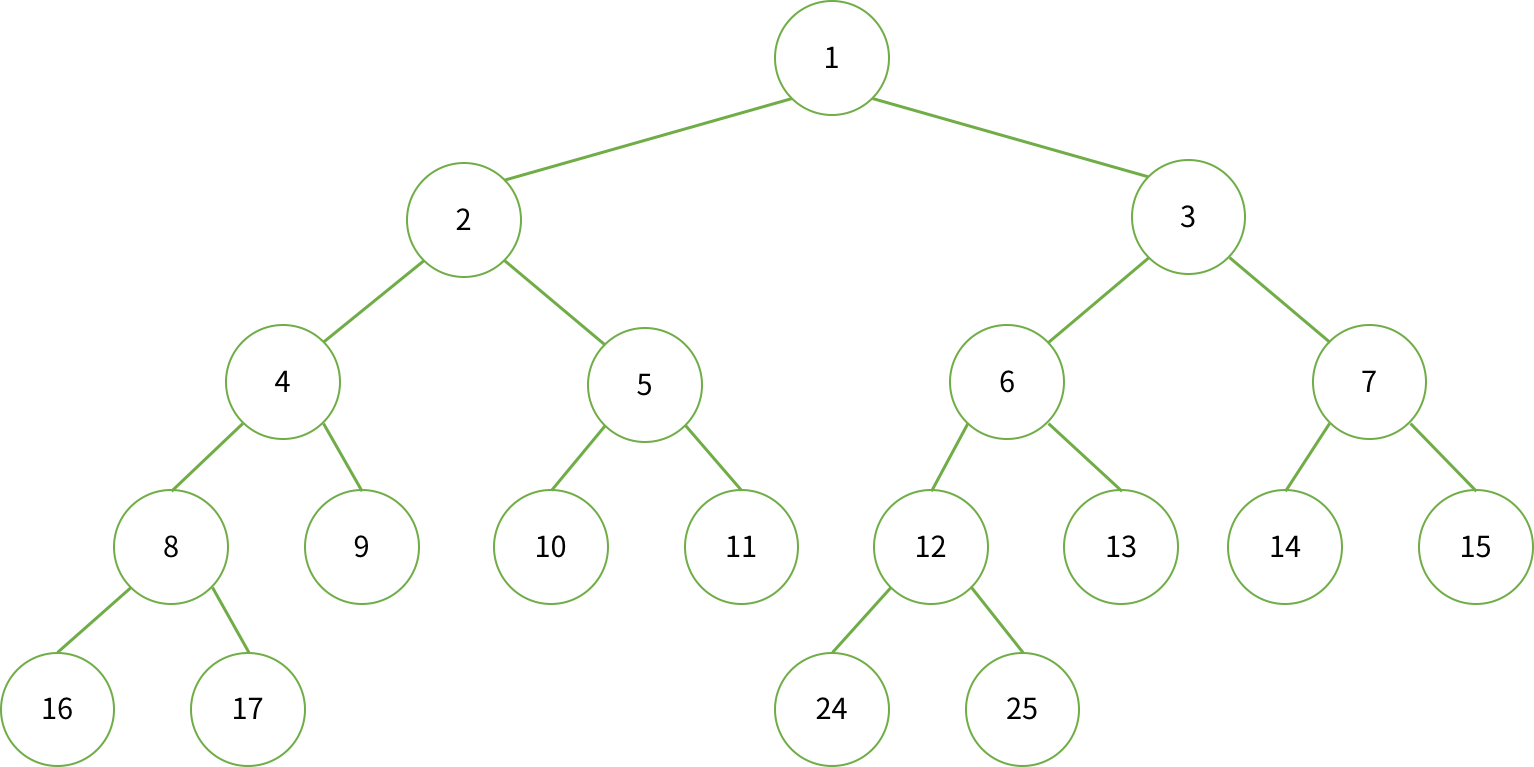
아래 코드를 통해 배열 p가 있을 때 세그먼트 트리 range를 구해보자.
이때 range의 크기는 p의 크기의 4배 정도로 초기화 해줘야 한다.
참고할 점은, 세그먼트 트리의 왼쪽 자손은 현재 노드*2, 오른쪽 자손은 현재 노드*2 +1이다.
즉 left = node*2, right = node*2 + 1로 인덱싱하면 된다.
배열 p의 값을 모두 입력받으면 init()함수를 통해 세그먼트 트리 range의 값을 구한다.
init에선 range의 모든 범위의 값을 구한다. 단말 노드까지 간다면 그 노드에 p의 값을 넣고
단말노드가 아니라면 왼,오른쪽 자손의 값을 더하는 게 전부이다. 어렵지 않다.
query함수는 구하고자 하는 트리의 범위의 값을 구해준다.
2~6까지의 값을 구하고자 하면 루트부터 내려가며 해당하는 범위의 값들을 더해 반환해준다.
update함수는 원본 배열 p의 값에 변경이 있을시 세그먼트 트리 range의 값도 최신화해주는 함수이다.
idx에 해당하는 단말노드의 값을 변경해준 후 그 부모노드들을 차례대로 update해주면 된다.
chosh95/STUDY
프로그래밍 문제 및 알고리즘 정리. Contribute to chosh95/STUDY development by creating an account on GitHub.
github.com
C++ 코드
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int N, M, K;
int a, b, c;
int p[1000001];
vector<int> range;
int init(int left, int right, int node) {
//단말노드인 경우 값 저장
if (left == right) return range[node] = p[left];
int mid = (left + right) / 2;
//node의 값은 좌,우 자손들의 구간 합
return range[node] = init(left, mid, node * 2) + init(mid + 1, right, node * 2 + 1);
}
int query(int left, int right, int node, int nodeLeft, int nodeRight) {
if (nodeRight < left || right < nodeLeft) return 0; //구하려는 구간에 포함되지 않는 경우
if (left <= nodeLeft && nodeRight <= right) return range[node]; //구간에 완전히 포함된 경우
int mid = (nodeLeft + nodeRight) / 2;
//좌,우 자손들의 구간합을 모두 합해 반환.
return query(left, right, node * 2, nodeLeft, mid) + query(left, right, node * 2 + 1, mid + 1, nodeRight);
}
void update(int idx, int newValue, int node, int nodeLeft, int nodeRight) {
if (idx < nodeLeft || nodeRight < idx) return; //바꾸려는 idx 범위밖인 경우
if (nodeLeft == nodeRight) { //바꾸려는 idx에 온 경우
range[node] = newValue; //값 변경
return;
}
int mid = (nodeLeft + nodeRight) / 2;
update(idx, newValue, node * 2, nodeLeft, mid);
update(idx, newValue, node * 2 + 1, mid + 1, nodeRight);
range[node] = range[node * 2] + range[node * 2 + 1]; //좌,우 자손들의 값을 최신화해준 후 다시 구간합 계산
}
int main()
{
cin >> N >> M >> K;
for (int i = 0; i < N; i++) cin >> p[i];
range.resize(N * 4);
init(0, N - 1, 1);
for (int i = 0; i < M + K; i++) {
cin >> a >> b >> c;
if (a == 1) {
update(b - 1, c, 1, 0, N - 1);
}
else {
cout << query(b - 1, c - 1, 1, 0, N - 1) << "\n";
}
}
}'알고리즘 > 기본 알고리즘' 카테고리의 다른 글
| 정렬 알고리즘(선택, 삽입, 버블, 머지, 퀵) (0) | 2020.04.23 |
|---|---|
| disjoint-set (Union-Find) (0) | 2020.02.15 |
| 힙(Heap) (0) | 2020.02.12 |
| KMP 알고리즘 (0) | 2020.02.04 |
| 큐, 스택과 덱 (0) | 2020.02.03 |